สวัสดีคอแทงหวยที่น่ารักทุกท่าน ยินดีต้อนรับทุกท่าน เข้าสู่ เว็บแทงหวยออนไลน์ 999LUCKY157
เว็บพนันหวยอันดับ 1 ที่ดีที่สุดในยุคนี้ มาพร้อมระบบโพยหวยที่ทันสมัยที่สุด ฝากถอนอัตโนมัติ ไม่มีขั่นต่ำ
สวัสดีคอแทงหวยทุกท่าน ทั้งสมาชิกเก่าและสมาชิกใหม่ทุกท่าน ยินดีต้อนรับทุกท่าน เข้าสุ่ระบบ เว็บแทงหวยออนไลน์ 999LUCKY เว็บพนันหวยอันดับ 1 ที่ดีที่สุดและมาแรงที่สุดในไทย ณ ปัจจุบันนี้ ด้วยระบบเว็บที่ทันสมัยและได้รับมาตรฐานในการให้บริการหวยออนไลน์ระดับสากล มีระบบแทงหวยออนไลน์ที่ทันสมัย ควบคู่ไปกับระบบรักษาความปลอดภัยขั้นสูง ทางเรารับประกันถึงความปลอดภัยของท่าน ไม่ว่าจะเป็นข้อมูลหรือบัญชีส่วนตัวของท่าน จะถูกเก็บไว้เป็นความลับ เพราะเรามีทีมงานมืออาชีพที่เก่งที่สุดในไทยคอยดูแลท่านเป็นอย่างดี สมัครแทงหวยออนไลน์ ซื้อหวยออนไลน์ 999LUCKY เชื่อถือได้ 100%
999LUCKY เว็บแทงหวยออนไลน์ครบวงจรที่ดีที่สุด มีหวยออนไลน์ให้คุณเล่นอย่างครบครัน จบครบทุกเรื่องหวย ไม่ว่าจะหวยในไทยหรือหวยต่างประเทศ เว็บไซต์เรานำหวยทุกชนิดมาอยุ่ใน 999LUCKY ที่นี้ที่เดียว ไม่ว่าจะเป็น หวยรัฐบาล หวยเวียดนาม (หวยฮานอย) หวยลาว Huay หวยสิงคโปร์ หวยมาเลย์ หวยปิงปอง (หวยยี่กี) หวยหุ้นไทย หวยหุ้นต่างประเทศ และ หวยลัคกี้เฮง และหวยออนไลน์ตัวอื่นๆ อีกมากมาย เพราะว่าเว็บไซต์เราบริการหวยออนไลน์ที่ยิ่งใหญ่และเป็นเจ้าแรกๆ ในไทยเลยก็ว่าได้ แทงหวย ซื้อหวยออนไลน์ 999LUCKY ซื้อง่าย จ่ายจริง จ่ายเต็ม ได้เงินครบ โอนไว ถอนเงินง่าย ถูกแสนจ่ายแสน ถูกล้านจ่ายล้าน ไม่มีประวัติการโกง
ลูกค้าท่านใดเล่นได้เราก็จ่ายตามยอดจริง ไม่หักเปอร์เซ้น ฝากเงินแล้วเล่นได้จริง ถอนเงินออกจากระบบได้จริงและยังรวดเร็วทันใจที่สุดในบรรดาเว็บหวยที่มี และเรายังรองรับระบบเล่นผ่านมือถือสมาร์ทโฟนทุกรุ่น ไม่ว่าจะเป็นระบบ Android , IOS รวมไปถึงการเล่นบน PC , Browser , Windows สามารถเล่นได้ทุกที่ทุกเวลา แทงหวยออนไลน์ได้ตลอด 24 ชั่วโมง มาพร้อมระบบ ฝากถอนอัตโนมัติ ฝากถอนไม่มีขั่นต่ำ ปรับยอดเครดิตเร็วทันใจ ถอนเงินง่าย ถอนเงินออกได้จริง ตอบโจทย์สำหรับนักเสี่ยงโชคทั้งหลาย แทงหวยออนไลน์ ไม่มีอั้น จ่ายเต็ม จ่ายหนัก จ่ายสูง อัตรการจ่ายรางวัลสุงที่สุด ส่วนลดเยอะ ซื้อหวยออนไลน์ 999LUCKY การเงิน มั่นคง ปลอดภัย 100%
999LUCKY มิติใหม่แห่งวงการหวยออนไลน์ที่ดีที่สุดในไทย
- ระบบรักษาความปลอดภัยระดับเทพ
- ใช้ Cloud Server เต็มรูปแบบ
- ระบบ สำรองข้อมูลลูกค้าแบบ Ail Time ไม่ต้องกลัวว่าเงินจะหาย
- ฝากถอนได้โดยไม่มีขั่นต่ำ
- มีโปรโมชั่นและสิทธิพิเศษอีกมากมาย
- แทงหวยไม่มีขั่นต่ำ
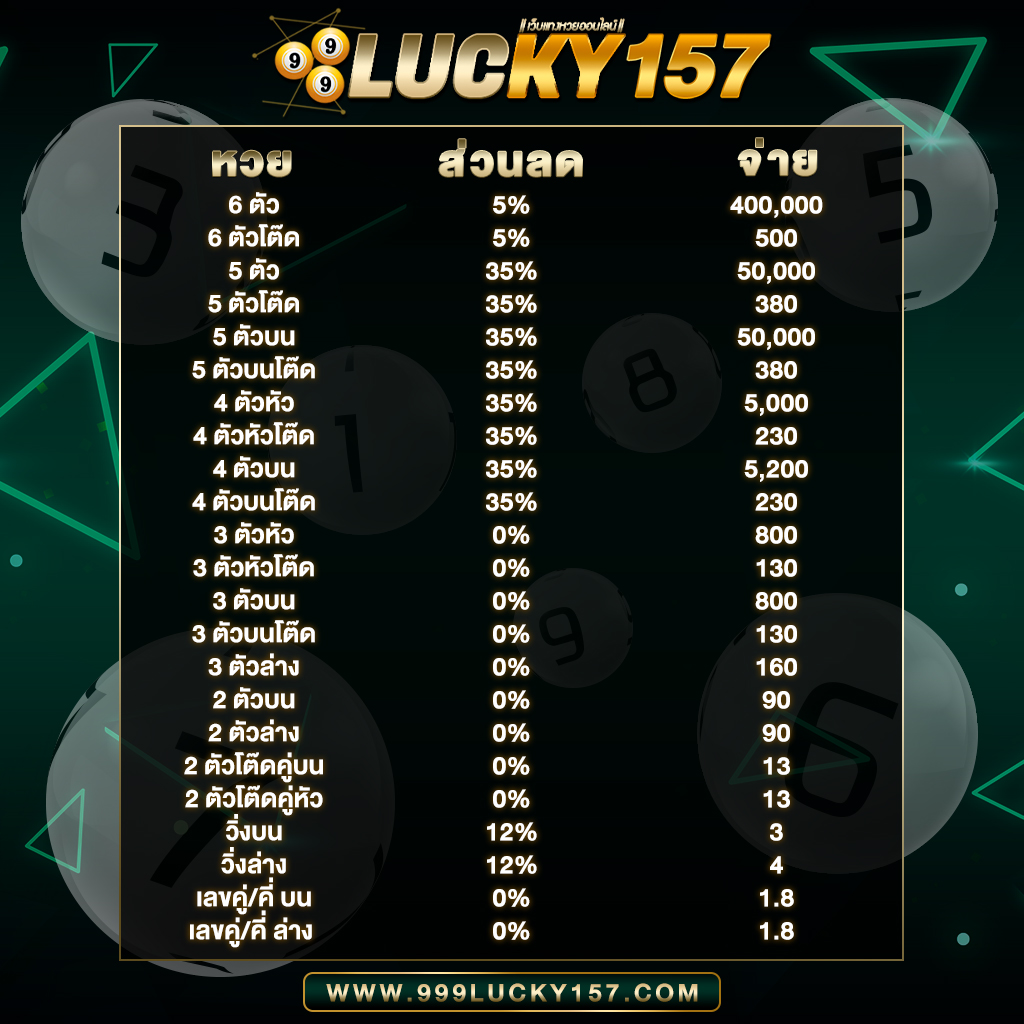
- อัตราการจ่ายสูงถึงบาทละ 800
- ระบบฝากถอนอัตโนมัติ รวดเร็ว ทันใจ
- รองรับการแทงหวยออนไลน์เต็มรูปแบบ
- ระบบติดต่อทางทีมงานเราได้ตลอด 24 ซม.
- ระบบแนะนำสมาชิก จ่ายค่าตอบแทนสูงสุดถึง 5%
- หวยปิงปอง ออกผลด้วยตัวเองได้
มาเปิดประสบการณ์ใหม่ๆไปกับการซื้อหวยออนไลน์กับ 999LUCKY
- อัตราจ่ายเยอะที่สุด สูงกว่าเว็บไหนๆ
- แทงเท่าไหร่ ถูกเท่านั้น หลักร้อยหรือหลักล้านเราก็พร้อมจ่าย
- จ่ายจริง จ่ายเต็ม ไม่เคยมีประวัติการโกงมาก่อน ไม่อาเปรียบท่านอย่างแน่นอน
- 999LUCKY เว็บเรา ซื่อสัตย์ โปร่งใส่ มั่นใจได้ถ้าเลือกซื้อหวยกับเรา
- การเงินท่านจะมั่นคงและปลอดภัย กว่าที่ใดๆ
- เปิดบริการให้เล่นกันยาวๆ ตลอด 24 ซม. ไม่มีปิด
- ซื้อหวยออนไลน์ จ่ายไม่อั้น รับทุกตัว ที่นี้ที่เดียว
- มีทีมงานคุณภาพสูง ที่มากไปด้วยประสบการณคอยดูแลคุณ
- เว็บเราไม่มีวันหยุดให้บริการ สามารถติดต่อสอบถามเราได้ตลอด 24 ซม.
- มีโปรโมชั่นและโบนัสแจกมากมาย และสิทธิพิเศษอีกมากมาย
- มีหวยออนไลน์ครบวงจรให้ท่านเลือกเล่นมากมาย เช่น หวยรับบาล ,หวยฮานอย,หวยลาว,หวยยี่กี,หวยหุ้น,หวยมาเลย์ และหวยตัวอื่นๆอีกมากมาย รวมหวยออนไลน์ที่มีทุกชนิดอยู่ที่ 999LUCKY ที่เดียว
แทงหวยออนไลน์ครบวงจรได้ที่ 999lucky-huay.com ที่นี้ที่เดียวในประเทศที่รวมหวยออนไลน์มากที่สุด
- หวยรัฐบาลไทย
- หวยลาว
- หวยเวียดนาม
- หวยลัคกี้เฮง
- หวยปิงปอง
- หวยหุ้นไทย
- หวยหุ้นต่างประเทศ
- หวยใต้ดิน
- หวยมาเลย์
- หวยสิงคโปร์
- หวยหุ้นดาวโจนส์
ซื้อหวยออนไลน์ ไม่ผ่านเอเยนต์ ไม่เสี่ยง ไม่ผ่านตัวแทนใดๆทั้งสิ้น ต้อง 999LUCKY เท่านั้น
แทงหวย 999LUCKY อัตราการจ่ายรางวัลสูงที่สุด แล้วท่านจะเป็นเศรษฐีคนต่อไป
หากท่านอยากเป็นนักแทงหวยที่เก่งที่สุด เข้ามาเปิดประสบการณ์ใหม่ๆไปกับ 999LUCKY
ติดต่อทีมงาน 999LUCKY / บริการงานโดย เฮียบิ๊ก @ ปอตเปต
E-Mail : [email protected]
ระบบจะจัดส่งให้ภายในเวลา 2-3 นาทีโดยอัตโนมัติ